Objective Practice Questions (MCQ)
1. In figure X is a point in the interior of square ABCD, AXYZ is also a square. If DY = 3 cm and AZ = 2 cm, then find BY.
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
2. It is given that ΔABC = ΔFDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(а) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E = 60°
(c) DE = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
3. D is a point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
(a) BD = CD
(b) BA > BD
(c) BD > BA
(d) CD > CA
4. In ΔABC, AB = AC and ∠B = 50°, then find ∠C.
(a) 50°
(b) 40°
(c) 80°
(d) 120°
5. In ΔABC, ∠C = ∠A and BC = 4 cm and AC = 5 cm, then find length of AB.
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 2.5 cm
Subjective Practice Questions
- In figure, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠QRS.
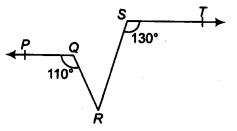
Solutions -Since PQ || ST [Given]
and EF || ST [Construction]
∴ PQ || EF and QR is a transversal
⇒ ∠PQR = ∠QRF [Alternate interior angles] But ∠PQR = 110° [Given]
∴∠QRF = ∠QRS + ∠SRF = 110° …(1)
Again ST || EF and RS is a transversal
∴ ∠RST + ∠SRF = 180° [Co-interior angles] or 130° + ∠SRF = 180°
⇒ ∠SRF = 180° – 130° = 50°
Now, from (1), we have ∠QRS + 50° = 110°
⇒ ∠QRS = 110° – 50° = 60°
Thus, ∠QRS = 60°.
2. In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 539 , find ∠DCE.
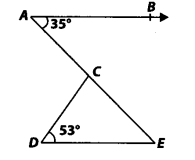
Solution:
AB || DE and AE is a transversal.
So, ∠BAC = ∠AED
[Alternate interior angles]
and ∠BAC = 35° [Given]
∴ ∠AED = 35°
Now, in ∆CDE, we have ∠CDE + ∠DEC + ∠DCE = 180°
{Angle sum property of a triangle]
∴ 53° + 35° + ∠DCE =180°
[∵ ∠DEC = ∠AED = 35° and∠CDE = 53° (Given)]
⇒ ∠DCE = 180° – 53° – 35° = 92°
Thus, ∠DCE = 92°
3. In figure, if PQ ⊥ PS, PQ||SR, ∠SQR = 2S° and ∠QRT = 65°, then find the values of x and y.
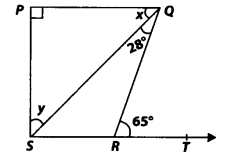
Solution:
In ∆ QRS, the side SR is produced to T.
∴ ∠QRT = ∠RQS + ∠RSQ
[Exterior angle property of a triangle]
But ∠RQS = 28° and ∠QRT = 65°
So, 28° + ∠RSQ = 65°
⇒ ∠RSQ = 65° – 28° = 37°
Since, PQ || SR and QS is a transversal.
∴ ∠PQS = ∠RSQ = 37°
[Alternate interior angles]
⇒ x = 37°
Again, PQ ⊥ PS ⇒ AP = 90°
Now, in ∆PQS,
we have ∠P + ∠PQS + ∠PSQ = 180°
[Angle sum property of a triangle]
⇒ 90° + 37° + y = 180°
⇒ y = 180° – 90° – 37° = 53°
Thus, x = 37° and y = 53°
4. Draw ray BL ⊥PQ and CM ⊥ RS
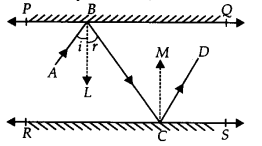
∵ PQ || RS ⇒ BL || CM
[∵ BL || PQ and CM || RS]
Now, BL || CM and BC is a transversal.
∴ ∠LBC = ∠MCB …(1) [Alternate interior angles]
Since, angle of incidence = Angle of reflection
∠ABL = ∠LBC and ∠MCB = ∠MCD
⇒ ∠ABL = ∠MCD …(2) [By (1)]
Adding (1) and (2), we get
∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD
i. e., a pair of alternate interior angles are equal.
∴ AB || CD.
