Chapter 5– Arithmetic Progressions

CONCEPTS FOR REVISION

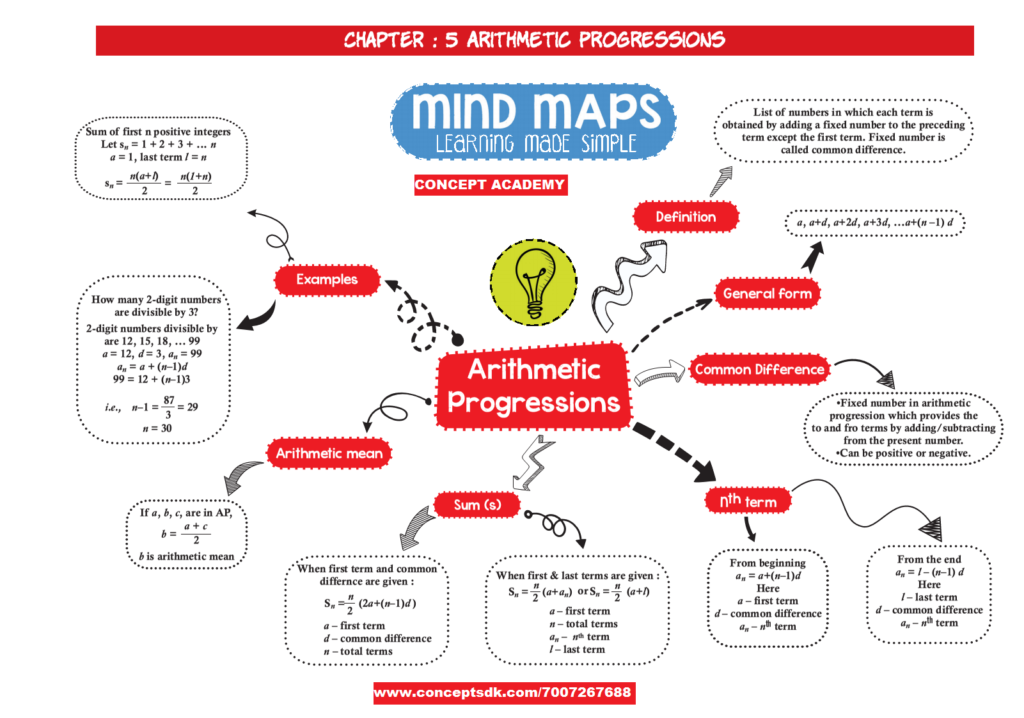
A Polynomial of the form p(x) = ax² + bx + c, where a 0 and a, b, c are real numbers and x is a real variable is called a quadratic polynomial.

An equation p(x) = 0, where p(x) is a quadratic polynomial is called a quadratic equation i.e. ax² + bx + c = 0, a 0.

Zeros of Quadratic Equations

Those values of x for which ax² + bx + c = 0 is satisfied are called zeros of quadratic equation.

Quadratic equation is classified into two categories

• Pure quadratic equation of type ax² + c = 0 by putting b = 0 in ax² + bx + c = 0

• Affected quadratic equation of type ax² + bx + c = 0, b 0.

Roots of Quadratic Equations

If α, β are the zeros of the polynomial ax² + bx + c. Then α, β are called roots of corresponding equation ax² + bx + c = 0

⇒ p(α) = p(β) = 0

i.e. aα² + bα + c = 0 and aβ² + bβ + c = 0

Pure quadratic ax² + c = 0 can be solved by any one of the following methods:

• By Taking square root • By factorisation

Affected quadratic equation can be solved by any one of the following method:

• By splitting middle term • By method of completing the square

D = b² – 4ac, is called the discriminant which decides the nature of roots.

• If D > 0, Roots are real and unequal.

• If D = 0, Roots are real and equal.

• If D < 0, No Real roots are possible.

The quadratic formula or Sridharacharya’s formula to find the roots of ax² + bx + c = 0 is

QUESTION BANK

Very Short Answer Question

The nth term of the AP a , 3a , 5a , … is
The common difference of the AP is

The first term of AP is p and the common difference is q , then its 10th term is
The value of x for which 2x, (x+10, and ( 3x+2) are the three consecutive terms of an AP, is
In an AP, if a = 3 5. , d = 0 and n = 101, then an will be
If the common difference of an AP is 5, then what is a₁₈-a₁₃ ?
Which term of an AP, 21, 42, 63, 84, … is 210?
The 4th term from the end of an AP -11, -8, -5 , ….., 49 is
6. The sum of first five multiples of 3 is
If the first term of an AP is -5 and the common difference is 2, then the sum of the first 6 terms is
An AP starts with a positive fraction and every alternate term is an integer. If the sum of the first 11 terms is 33, then the fourth term is
If the sum of the first 2n terms of 2, 5, 8, ………. is equal to the sum of the first n terms of 57, 59, 61, ………., then n is equal to
The 21th term of an AP whose first two terms are -3 and 4, is
The number of two digit numbers which are divisible by 3 is
If 7 times the 7th term of an AP is equal to 11 times its 11th term, then its term will be
If the nth term of an AP is 4n+1 , then the common difference is
The sum of 11 terms of an AP whose middle term is 30, is
Assertion: Common difference of the AP -5 , -1 , 3, 7, ………. is 4.

Reason: Common difference of the AP a, a+d, a+2d, ………. is given by

(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).

(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).

(d) Assertion (A) is false but reason (R) is true.

. The sum of first 20 terms of the AP 1, 4, 7, 10 …. is
If 4 times the 4th term of an AP is equal to 18 times the 18th term, then find the 22nd term.
If the first three terms of an AP are b, c and 2b, then find the ratio of b and c .
The nth term of an AP is (7-4n) , then what is its common difference?
Find the number of natural numbers between 102 and 998 which are divisible by 2 and 5 both.
In an AP, if the common difference d =− 4, and the seventh term a7 is 4, then find the first term
. Find the sum of first 8 multiples of 3
Find, how many two digit natural numbers are divisible by 7.
Is -150 a term of the AP 11, 8, 5, 2, …….?
Which of the term of AP 5, 2, – ,……1 is -49?
Find the first four terms of an AP Whose first term is -2 and common difference is – 2

What is the next term of an AP ?