NCERT LINE BY LINE QUESTIONS
- The escape speed of a body from the earth depends on
(1) Mass of the body
(2) The direction of projection
(3) The height of location from where the body is launched
(4) All of these
NCERT Practice Questions
- All planets move i elliptical orbits with the sun situated at one of the foci”. This law was given by
(a) Newton (b) keplar (c) Archimedesc (d) Pascal
2. Planet revolving round sun swept out equal area in equal time because
(a) Its linear momentum remain constant
(b) It angular momentum remain constent
(c) Its (linear + angular) momentum remain constant
(d) None of these
3. If earth pull moon with force F the moon pull the earth with force
(a) greater than F (b) less than F
(c) equal to F (d) none of these
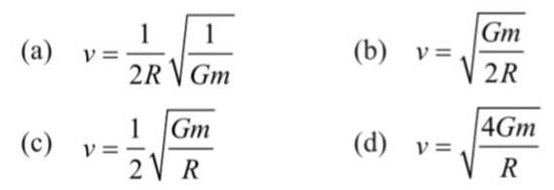
1. Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
2. The gravitational force between two point masses m1 and m2 at separation r is given by k m1 m2 /r2
The constant k
(A) Depends on system of units only
(B) Depends on medium between masses only
(C) Depends on both (A) and (B)
(D) Is independent of both (A) and (B)
3. Two sphere of mass m and M are situated in air and the gravitational force between them is F. The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be
(A) F (B) F/3 (C) F/9 (D) 3 F
4. Two planets have the same average density but their radii are R1 and R2 . If acceleration due to gravity on these planets be g1 and g2 respectively, then
(A) g1/g2 = R1/R2 (B) g1/g2 = R2/R1
(C) g1/g2 = R21/R22 (D) g1/g2 = R31/R32
5. An iron ball and a wooden ball of the same radius are released from a height ‘h’ in vacuum. The time taken by both of them to reach the ground is
(A) Unequal (B) Exactly equal
(C) Roughly equal (D) Zero
6. A body weighs 700 gm wt on the surface of the earth. How much will it weigh on the surface of a planet whose mass is 1/7 and radius is half that of the earth
(A) 200 gm wt (B) 400 gm wt
(C) 50 gm wt (D) 300 gm wt
7. The radius of the earth is 6400 km and g=10m/s2. In order that a body of 5 kg weighs zero at the equator, the angular speed of the earth is
(A) 1/80 radian/sec
(B) 1/400 radian/sec
(C) 1/800 radian/sec
(D) 1/1600 radian/sec
8. The radii of two planets are respectively and
and their densities are respectively
and
. The ratio of the accelerations due to gravity at their surfaces is
(A)
(B)
(C)
(D)
9. Radius of earth is around 6000 km. The weight of body at height of 6000 km from earth surface becomes
(A) Half (B) One-fourth
(C) One third (D) No change
10. A body weighs 200 N on the surface of the earth. How much will it weight halfway down to the center of the earth ?
(A) 150 N (B) 200 N
(C) 250 N (D) 100N
11. An object weights 72 N on earth. Its weight at a height of R/2 from earth is
(A) 32 N (B) 56 N
(C) 72 N (D) Zero
12. The depth d at which the value of acceleration due to gravity becomes times the value at the surface, is [R = radius of the earth]
(A) (B)
(C) (D)
13. What will be the acceleration due to gravity at height h if h >> R. Where R is radius of earth and g is acceleration due to gravity on the surface of earth
(A) (B)
(C) (D)
14. The moon’s radius is 1/4 that of the earth and its mass is 1/80 times that of the earth. If g represents the acceleration due to gravity on the surface of the earth, that on the surface of the moon is
(A) g/4 (B) g/5 (C) g/6 (D) g/8
15. The masses of two planets are in the ratio 1 : 2. Their radii are in the ratio 1 : 2. The acceleration due to gravity on the planets are in the ratio
(A)1 : 2 (B) 2 : 1 (C)3 : 5 (D)5 : 3
16. The masses and radii of the earth and moon are and
respectively. Their centres are distance d apart. The minimum velocity with which a particle of mass m should be projected from a point midway between their centres so that it escapes to infinity is
(A)
(B)
(C)
(D)
17. There are two bodies of masses 100 kg and 10000 kg separated by a distance 1 m. At what distance from the smaller body, the intensity of gravitational field will be zero
(A) (B)
(C) (D)
18. Escape velocity on a planet is . If radius of the planet remains same and mass becomes 4 times, the escape velocity becomes
(A) (B)
(C) (D)
19. Energy required to move a body of mass m from an orbit of radius 2R to 3R is
(A) (B)
(C) (D)
20. The escape velocity on earth is 11.2 km/s. On another planet having twice radius and 8 times mass of the earth, the escape velocity will be
(A) 3.7 km/s (B) 11.2 km/s
(C) 22.4 km/s (D) 43.2 km/s
21. Given mass of the moon is 1/81 of the mass of the earth and corresponding radius is 1/4 of the earth. If escape velocity on the earth surface is 11.2 km/s, the value of same on the surface of the moon is
(A) 0.14 km/s (B) 0.5 km/s
(C) 2.5 km/s (D) 5 km/s
22. The escape velocity for a body projected vertically upwards from the surface of earth is 11 km/s. If the body is projected at an angle of 45o with the vertical, the escape velocity will be
(A) (B)
(C) 22 km/s (D) 11 km/s
23. If the radius of a planet is four times that of earth and the value of g is same for both, the escape velocity on the planet will be
(A) (B)
(C) (D) None
24. For a satellite moving in an orbit around the earth, the ratio of kinetic energy to potential energy is
(A) 2 (B) (C)
(D)
25. If and
represent the escape velocity and orbital velocity of a satellite corresponding to a circular orbit of radius R, then
(A)
(B)
(C)
(D) and
are not related
26. The least velocity required to throw a body away from the surface of a planet so that it may not return is (radius of the planet is
(A) (B)
(C) (D)
27. Two satellites A and B go round a planet P in circular orbits having radii 4R and R respectively. If the speed of the satellite A is 3V, the speed of the satellite B will be.
(A) 12 V (B) 6 V
(C) (D)
28. Orbital velocity of an artificial satellite does not depend upon
(A) Mass of the earth
(B) Mass of the satellite
(C) Radius of the earth
(D) Acceleration due to gravity
29. For a satellite escape velocity is 11 km/s. If the satellite is launched at an angle of 60° with the vertical, then escape velocity will be
(A) 11 km/s (B) km/s
(C) km/s (D) 33 km/s
30. The weight of an astronaut, in an artificial satellite revolving around the earth, is
(A) Zero
(B) Equal to that on the earth
(C) More than that on the earth
(D) Less than that on the earth
31. The distance between centre of the earth and moon is 384000 km. If the mass of the earth is and
. The speed of the moon is nearly
(A) 1 km/sec (B) 4 km/sec
(C) 8 km/sec (D) 11.2 km/sec
32. Select the correct statement from the following
(A) The orbital velocity of a satellite increases with the radius of the orbit
(B) Escape velocity of a particle from the surface of the earth depends on the speed with which it is fired
(C) The time period of a satellite does not depend on the radius of the orbit
(D) The orbital velocity is inversely proportional to the square root of the radius of the orbit
33. If the gravitational force between two objects were proportional to 1/R (and not as where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
(A) (B)
(C) (D) 1/R
34. Potential energy of a satellite having mass ‘m’ and rotating at a height of from the earth surface is
(A) (B)
(C) (D)
35. If satellite is shifted towards the earth. Then time period of satellite will be
(A) Increase
(B) Decrease
(C) Unchanged
(D) Nothing can be said
(SECTION-B)
36. The time period of a satellite of earth is 5 hours. If the separation between the earth and the satellite is increased to four times the previous value, the new time period will become
(A) 20 hours (B) 10 hours
(C) 80 hours (D) 40 hours
37. The distance of neptune and saturn from sun are nearly and
meters respectively. Assuming that they move in circular orbits, their periodic times will be in the ratio
(A) (B) 100
(C) (D)
38. The figure shows the motion of a planet around the sun in an elliptical orbit with sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If and
represent the time for the planet to move from a to b and d to c respectively, then
(A) (B)
(C) (D)
39. The period of a satellite in a circular orbit of radius R is T, the period of another satellite in a circular orbit of radius 4R is
(A) 4T (B) T/4
(C) 8T (D) T/8
40. A satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at a distance of 2r from the earth’s centre. Their time periods are in the ratio of
(A) 1 : 2 (B) 1 : 16
(C) 1 : 32 (D)
41. If the radius of earth’s orbit is made 1/4, the duration of an year will become
(A) 8 times (B) 4 times
(C) 1/8 times (D) 1/4 times
42. The radius of orbit of a planet is two times that of the earth. The time period of planet is
(A) 4.2 years (B) 2.8 years
(C) 5.6 years (D) 8.4 years
43. Kepler’s second law (law of areas) is nothing but a statement of
(A) Work energy theorem
(B) Conservation of linear momentum
(C) Conservation of angular momentum
(D) Conservation of energy
44. If the radius of the earth were to shrink by 1% its mass remaining the same, the acceleration due to gravity on the earth’s surface would
(A) Decrease by 2%
(B) Remain unchanged
(C) Increase by 2%
(D) Increase by 1%
45. A body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be
(A) mgR (B)
(C) 2 mgR (D)
46. Which of the following graphs represents the motion of a planet moving about the sun
(A) (B)
(C) (D)
47. Assertion : If a pendulum is suspended in a lift and lift is falling freely, then its time period becomes infinite.
Reason : Free falling body has acceleration equal to acceleration due to gravity.
(A) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(B) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(C) If assertion is true but reason is false.
(D) If the assertion and reason both are false.
48. The escape velocity from the Earth’s surface is . The escape velocity from the surface of another planet having a radius, four times that of Earth and same mass density is:
(A) (B) 2
(C) 3
(D) 4
49. A body of mass 60g experiences a gravitational force of 3.0N , when placed at a particular point. The magnitude of the gravitational field intensity at that point is
(A) 50 N kg-1 (B) 20 N kg-1
(C) 180 N kg-1 (D) 0.05 N kg-1
50. Match the statements of Column A with those of Column B.
| Column A | Column B |
| (A) Kepler’s law | (p) |
| (B) The value of the ‘g’ on the surface of planet | (q) |
| (C) The value of ‘g’ at certain height from the surface of the earth | (r) T2µR3 |
| (D) Escape velocity | (s) |
(A) a → r; b → p; c → q; d → s
(B) a → r; b → q; c → s; d → p
(C) a → r; b → p; c → s; d → q
(D) a → p; b → r; c → s; d → q
